Powiedz mi, to zapomnę. Naucz mnie, to może zapamiętam. Zaangażuj mnie, to się nauczę.
Benjamin Franklin
Wstęp
Mamy świadomość, że kształtowanie właściwych intuicji matematycznych konieczne jest już od wczesnych etapów edukacji. Myślenie matematyczne jest sposobem pojmowania świata, jego elementów i relacji między nimi. Jest to coś zupełnie innego niż schematyczne rozwiązywanie zadań, wykonywanie operacji i stosowanie procedur. To dynamiczny proces, który rozszerza nasze rozumienie, gdyż pozwala nam radzić sobie z coraz bardziej złożonymi ideami.
Mogen Niss[1], formułując osiem fundamentów kompetencji matematycznych, na pierwszym miejscu stawia właśnie myślenie matematyczne, które utożsamia z umiejętnością stawiania pytań (Niss, 2003). Pozostałe fundamenty to:
- Formułowanie i rozwiązywanie problemów matematycznych.
- Modelowanie matematyczne, którego zakres obejmuje komunikowanie.
- Rozumowanie matematyczne.
- Reprezentowanie bytów matematycznych czyli rozumienie, interpretowanie.
- Posługiwanie się matematyczną symboliką i formalizmami.
- Matematyczne komunikowanie się czyli rozumienie matematycznych komunikatów.
- Używanie pomocniczych narzędzi.
Kształcąc myślenie matematyczne, oczywiście w odpowiedni i efektywny sposób, wyrabiamy u ucznia lub każdej innej osoby rozwijającej się cechy myślenia krytycznego. Działania te są możliwe i pożądane na każdym etapie rozwoju intelektualnego, o których wspomina Piget[2]. Na każdym z tych etapów konieczne jest jednak użycie innych metod i narzędzi, właściwych do możliwości percepcyjnych danego etapu rozwojowego.
Krytyczne myślenie obejmuje szereg skumulowanych i powiązanych zdolności, dyspozycji i innych zmiennych, takich jak: motywacja, kryteria, kontekst i wiedza. Kształtowanie krytycznego myślenia opiera się na doświadczeniach, na przykład obserwowaniu czegoś niezwykłego lub nietypowego, a następnie na drodze różnych form dochodzeń, które zakładają obserwację, wnioskowanie, argumentację, dowodzenie, testowanie wniosków oraz refleksję, dochodzenie do sformułowania wniosków i odpowiedzi.
Na poniższym wykresie można wyraźnie dostrzec, jak bardzo wzrost kompetencji charakterystycznych dla myślenia matematycznego wpływa na rozwój umiejętność myślenia krytycznego (ryc. 1).
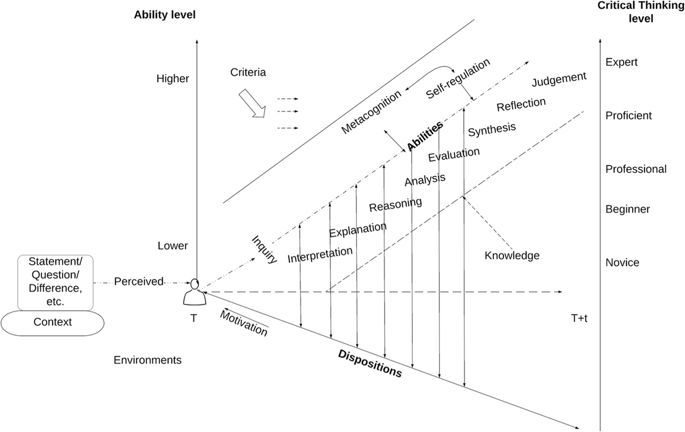
Rozwój myślenia krytycznego często zaczyna się od prostych doświadczeń, takich jak: obserwowanie różnic, napotykanie zagadkowych pytań lub problemów, kwestionowanie wypowiedzi innych osób, co następnie prowadzi do bardziej złożonych doświadczeń wykorzystujących umiejętności myślenia matematycznego wyższego rzędu, tj. logiczne rozumowanie, kwestionowanie założeń, rozważanie i ocena alternatywnych wyjaśnień.
Do uruchomienia i kształtowania tego typu myślenia konieczna jest wiedza oraz motywacja do rozwoju, właściwe narzędzia i dobrze zadane pytania i zadania przez nauczyciela (Ma, Spector, 2019).
Dlaczego geometria?
Do zrozumienia tej najstarszej dyscypliny matematyki oraz swobodnego posługiwania się jej pojęciami potrzeba wielu kompetencji, takich jak: wyobraźnia, logiczne i racjonalne wnioskowanie, dowodzenie, stawianie hipotez, umiejętne czytanie treści zadań matematycznych i – do tego – poruszanie się w obszarze wszystkich reprezentacji języka matematycznego: słowa, symbolu i grafiki. Hans Freudenthal w 1966 napisał: „Geometria grecka była pierwszym właściwym ucieleśnieniem idei matematyki. Chociaż działalność matematyczna, zarówno w algebrze, jak i geometrii, rozpoczęła się dwa czy trzy tysiące lat przed Euklidesem, wyrazy takie, jak twierdzenie, założenie, dowód, analiza, teoria, aksjomat, postulat, definicja i pojęcia, które one oznaczają, są wynalazkiem matematyki greckiej” (Freudenthal, 1966).
Zaprezentowane poniżej przykłady praktyk i pomysłów na rozwijanie i kształtowanie myślenia krytycznego poprzez zabawę geometrią, są efektem współpracy z moimi twórczymi studentami[1], a także ze środowiskiem nauczycieli, metodyków, matematyków i informatyków. Aktywizują oni nieustannie moją motywację do generowania nowych pomysłów na zajęcia z przyszłymi nauczycielami matematyki i informatyki oraz ukazują deficyty i potrzeby współczesnej szkoły.
Prowokowanie intuicji i wyobraźni
Rzeczywistość dostarcza nam bodźców wzrokowych, dotykowych i motorycznych. Nauczyciele i rodzice powinni dokładać wszelkich starań, by rozbudzać w dzieciach właściwe pojmowanie przestrzeni. Kształtuje się ono poprzez zabawę, między innymi: układanie klocków, lepienie z plasteliny, układanie puzzli, czy składanie origami.
Origami
Teresa Gołąb uważa, że origami pozwala prowokować i kształtować następujące umiejętności:
- stawianie hipotez i ich weryfikację, czyli wdraża do rozwiązywania problemów oraz pokonywania trudności z tym związanych,
- tworzenie form geometrycznych,
- uchwycenie proporcji i struktury,
- rozwijanie myślenia konstrukcyjnego oraz
- rozwijanie wyobraźni przestrzennej (Gołąb, 1993).
Dzięki technice origami dzieci poznają i utrwalają pojęcia geometryczne. Zginają i obserwują, z każdym kolejnym ćwiczeniem są bardziej świadome własności figur płaskich, stopniowo zamieniają potoczne słownictwo na język matematyki. Efekty poszczególnych przejść opisują już nie jako zgięcie lub linia, ale prosta, przekątna, bok, odcinek prostopadły lub równoległy. Szukają cech wspólnych wykonywanych przedmiotów, porównują je pod względem wielkości i kształtu. Precyzyjniej określają wzajemne położenie prostych, mierzą długości odcinków i wielkości kątów, jakie powstały w wyniku odpowiednich zgięć.
Origami z kół może być doskonałą nauką proporcji i wyobraźni przestrzennej przez zabawę przez dzieci przedszkolne i wczesnoszkolne.

Zbudować możemy wiele, między innymi, sześcian oraz… no właśnie, kto zgadnie, co znajduje się na pozostałych rysunkach?

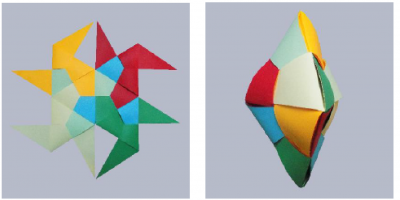
Wiernie z komendami z instrukcji złóżmy z naszymi uczniami sześciokąt foremny.



A później przekonajmy się, że powstała w ten sposób figura rzeczywiście jest wielokątem foremnym.
Podobnie możemy postąpić, chcąc z użyciem origami dokonać podziału kwadratu na trzy równe części.
Wycinanki
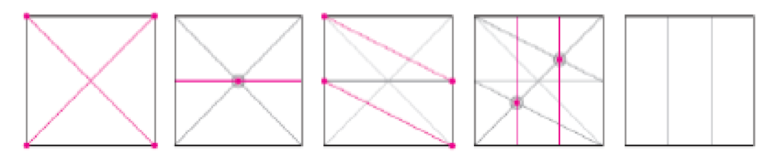
Już wiemy, że z odpowiednio złożonej kartki papieru jednym prostym cięciem da się wyciąć dowolny wielokąt (Ciesielska, Kowalczyk, 2016).
Jak zatem uzyskać następujące kształty?
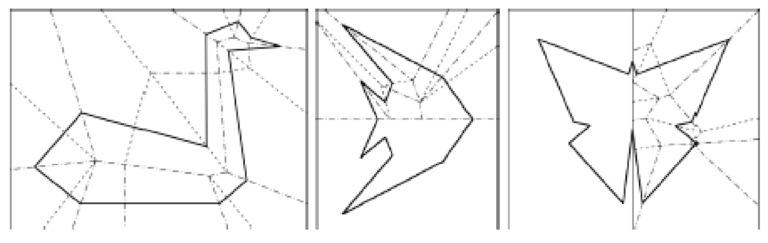
Shapes
Mamy dziś dostęp do wielu narzędzi IT, które powinny wspierać uczniów szczególnie w procesie stawiania i rozwiązywania problemów matematycznych. W geometrii jednym z warunków poprawnie określonych danych i zmiennych zadania oraz postawionego problemu jest umiejętność właściwej interpretacji tekstu matematycznego oraz osadzenia pojęć na rysunku pomocniczym. Gdzie znajduje się punkt, o którym mowa w zadaniu? A gdzie znajduje się prosta? Czy to właściwy odcinek? Jak odnaleźć i narysować przekrój bryły, o którym mowa w zadaniu? To tylko nieliczne z pytań co dzień zadawane przez uczniów.
Jednym z programów, który powstał właśnie w celu wsparcia widzenia w przestrzeni, wsparcia uczniów w poprawnym rysowaniu i interpretowaniu rysunków pomocniczych jest aplikacja Shapes[1].
Shapes 3D – Geometry Learning
Aplikacja Geometry Learning jest odpłatna i dostępna dla iOS, Web, Chrome OS, macOS, Android oraz Windows.
Aplikacja nie służy do samodzielnego rysowania, a jedynie do obserwacji i wizualizacji brył zaproponowanych w programie. W kategorii graniastosłupy jest możliwy wybór pomiędzy jedenastoma możliwościami, natomiast w kategorii ostrosłupy – ośmioma. Wszystkie bryły są bryłami prostymi. Podczas pracy z aplikacją można dokonywać zmiany trybu kolorowania ścian, sprawdzenia nazwy bryły podstawowych informacji, tj. liczby ścian, wierzchołków oraz krawędzi.
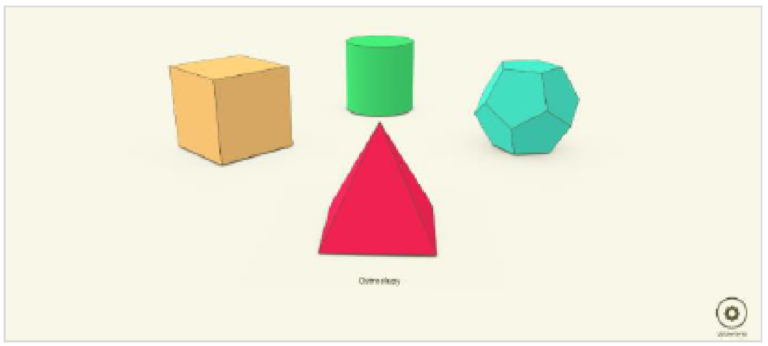
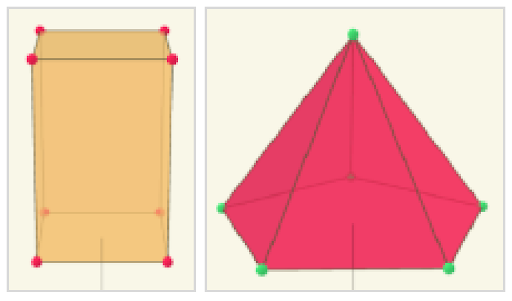
Każdą z brył można rozłożyć i w efekcie uzyskać jej siatkę, a podczas animacji można dokładnie zaobserwować, wzdłuż których krawędzi bryła została rozcięta.
Ponadto aplikacja umożliwia samodzielne zbudowanie siatki oraz zapisanie jej do wydruku, poprzez dodanie motylków umożliwiających sklejenie bryły.

Shapes 3D – Geometry Drawing
Geometry Drawing jest darmową aplikacją dostępną dla iOS, Web oraz Android. Proponowana jest dla starszych klas szkoły podstawowej, czyli klasy 7. i 8.
Pierwszą funkcją programu jest opcja zaznaczania punktów – można oznaczyć wierzchołki bryły, którym automatycznie przypisywane są litery Łącząc utworzone wcześniej punkty, można poprowadzić w bryłach dowolne odcinki, na przykład różnego rodzaju wysokości lub przekątne umożliwia wyróżnienie podstawy, ściany, przekroju lub stworzenie dowolnej powierzchni. Aplikacja umożliwia zmianę trybu widoku, w jakim obserwuje się bryłę. Jako domyślny ustawiony jest widok perspektywiczny, który najbardziej przypomina to, co obserwuje się w rzeczywistości, co oznacza, że obraz posiada głębię. Można zmienić również widok na izometryczny.
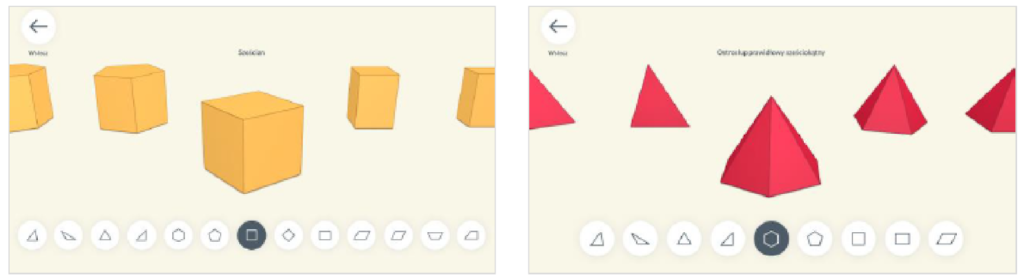
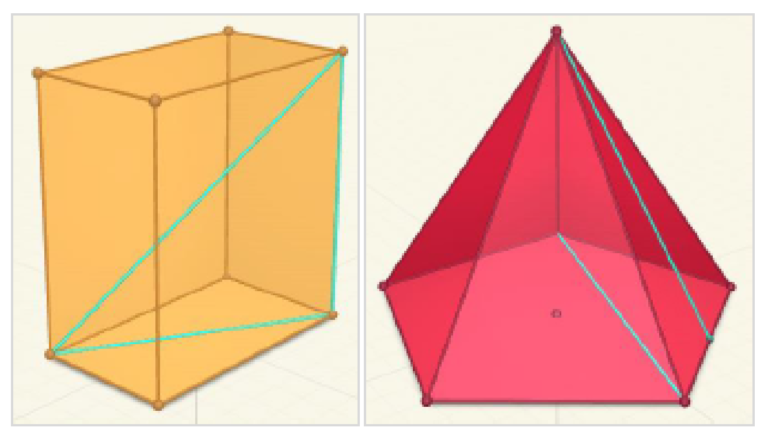
Najciekawszym widokiem jest tak zwany Merge Cube. Aby móc korzystać z tej opcji, należy zaopatrzyć się w specjalną czarną kostkę, która otwiera przed nami bogactwo rozszerzonej rzeczywistości.

Podważanie intuicji
Rozbudzanie nieustannej ciekawości, prowokowanie do badania i odkrywania zależności, które czasami trudno ogarnąć jednym rzutem myśli, z którymi często trudno jest się tak po prostu zgodzić.
Wiele ciekawych zagadek i pomysłów na interesującą lekcję lub dyskusję znaleźć można w najstarszym matematycznym czasopiśmie dla młodzieży o umysłach ścisłych i nie tylko, jest Delta (Delta Edu). Co roku na Wydziale Matematyki i Informatyki UAM mamy możliwość i ogromną przyjemność spotkać redaktorów „Delty”, wysłuchać ich wykładów i popracować na warsztatach (Dzień Delty).
Rozważymy tu dwa zadania wraz z rozwiązaniami (Jaszuńska, 2017):
- Czy można wyciąć w kartce dziurę w kształcie monety 1-groszowej, a następnie przełożyć przez tę dziurę monetę 1-złotową?
- Mamy kartkę o wymiarach 10 cm × 10 cm i nożyczki. Czy można wyciąć taką dziurę, przez którą przejdzie człowiek?
Te dwa zadania zostały właśnie przedyskutowane na łamach czasopisma „Delta”.
Rozwiązanie zadania nr 1 (Jaszuńska, 2017)
Po wycięciu dziury warto utworzyć cztery pomocnicze zagięcia. Następnie kartkę złożyć w pół wzdłuż jednego z nich i odciągnąć od siebie końce dziury, uzyskując dłuższy, wąski otwór.
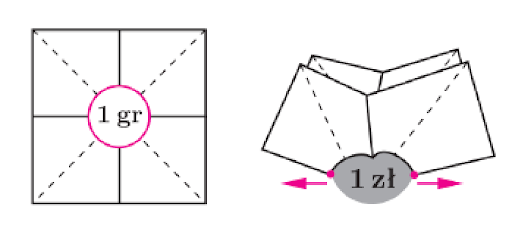
Rozwiązanie zadania nr 2
Kartkę można na przykład najpierw rozciąć wzdłuż spiralnej linii, uzyskując bardzo długi, poskręcany pasek, a następnie naciąć wzdłuż prawie całej długości tego paska, otrzymując w nim wystarczająco dużą dziurę.
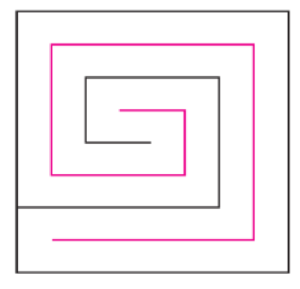
Zachęcam do rozwiązania następujących problemów:
Zadanie 3. A czy potrafisz wyobrazić sobie, jaką wysokość będzie miała chusteczka papierowa, jeżeli moglibyśmy ją złożyć 50 razy na pół, na pół, na pół, itd. Czy zmieści się w Twojej kieszeni?
Zadanie 4. A czy potrafisz szybko odpowiedzieć, jaką najmniejszą liczbę klocków potrzebujesz do złożenia budowli opisanej na rysunkach poniżej.
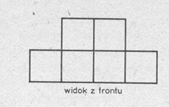
Zadanie 5. Czy możliwa jest jazda na rowerze z kwadratowymi kołami?
Uzasadnianie i kwestionowanie wypowiedzi innych osób
Zofia Krygowska, twórczyni polskiej dydaktyki matematyki, szczególną uwagę zwracała na rolę błędu w procesie nauczania-uczenia się, nazywając go „błogosławionym”. Akcentowała zdecydowanie, by nie unikać dyskusji z uczniami o błędach, szczególnie tych, które oni sami popełniają. G. Polaya dodaje do tego jeszcze kolejne ważne stwierdzenie: „rzuć okiem wstecz”, czyli przyjrzyj się temu, co zrobiłeś, przedyskutuj popełnione błędy i postaraj się odnaleźć inną, efektywną metodę rozwiązania zadania.
Bardzo często wytwory naszych uczniów mogą stanowić doskonały materiał do dalszej pogłębionej pracy.
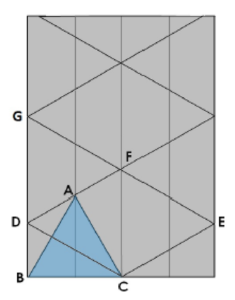
Zadanie[1]
Sprawdź, jaką częścią prostokąta jest pole zacieniowanej figury.
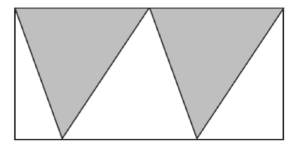
Odpowiedzi oczywiście mogą być bardzo różne: poprawne, niepoprawne, z błędem rachunkowym, w nadmiarze zawierzające rysunkowi pomocniczemu, bez potrzeby przeprowadzenia poprawnego wnioskowania. Poniższe wybrane odpowiedzi uczniów bardzo wyraźnie prowokują do zorganizowania z uczniami pogłębionej dyskusji nad tym, jakie mogą być sposoby rozwiązania tego zadania, jaką rolę pełni rysunek, czy może on nam w jakiś sposób przeszkodzić w uruchomieniu formalnych procedur, czy „widać” wystarczy, by uznać, że zadanie zostało rozwiązane?
Prace uczniów
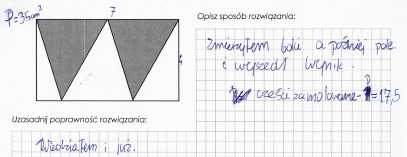
Istnieje jeszcze wiele różnych pomysłów na to, by – bez względu na to, czy pracujemy zdalnie czy też twarzą w twarz – prowokować myślenie krytyczne, kształtować myślenie matematyczne pobudzać uczniów do świadomej i aktywnej pracy. Ze względu na ograniczoną pojemność artykułu zaprezentowano jedynie kroplę z morza pomysłów i praktyk. Powodzenia!
"Wszelkie nauczanie jest najlepiej osiągane w formie rozrywki. Pozwólmy, aby dziecięca praca i nauka były rodzajem zabawy."
Platon
Przypisy
- Emerytowany pracownik Röskilde University, matematyk, żywo zainteresowany problemami edukacji matematycznej, prowadzący badania dotyczące problemów uzasadniania w edukacji matematycznej, zastosowań matematyki oraz modelowania. Członek Komisji Edukacji w Europejskim Towarzystwie Matematycznym.
- Szwajcarski psycholog rozwojowy, biolog, żył w latach (1896-1980), twórca kompleksowej teorii o naturze i rozwoju ludzkiej inteligencji.
- W pracy zaczerpnięte zostały fragmenty pomysłów dydaktycznych opisanych w pracach dyplomowych moich studentek: Anny Suszek, Joanny Polcyn, Doroty Rosiak oraz Moniki Kędzierskiej.
- Shapes zostało wprowadzone w 2009 roku przez polską firmę Learn Teach Explore. Nad jej poprawnością merytoryczną czuwa m.in. dr Edyta Juskowiak z Wydziału Matematyki i Informatyki Uniwersytetu im. Adama Mickiewicza w Poznaniu. Tam też aplikacja została zweryfikowana i zatwierdzona. Oprogramowanie Shapes dostępne jest w 17 wersjach językowych i podzielone jest na dwie aplikacje: Geometry Learning oraz Drawing. Każda z aplikacji skupia się na innych możliwościach, co powoduje, że razem tworzą bogaty zbiór funkcjonalności. Oficjalna strona aplikacji Shapes: https://shapes.learnteachexplore.com/
- Jest to jedno z zadań, które Autorka tego artykułu wykorzystuje w swoich badaniach mających na celu m.in. opisanie przejawów myślenia formalnego i gotowości do prowadzenia rozumowań dowodowych przez uczniów szkoły podstawowej klas 7. i 8.
Filmy do słownego/medialnego opracowania
Wyniki badań nad czynnikami determinującymi skuteczność uczenia się/nauczania (oczywiście obok potencjału intelektualnego i emocjonalnego uczniów) wskazują na cztery czynniki najbardziej znaczące. Są to: (a) relacje między uczniami a nauczycielem (Hattie, 2012); (b) aktywność – przede wszystkim – fizyczna (a tutaj głównie dłonie – G. Lundberg, 2013); (c) operowanie słowem – ciągle najważniejsze dla rozwoju intelektualnego i moralnego (Hammond 2019; Rutherford, 2019, Everett, 2018, Dylak, 2017 ), ale musimy dodać: opartym na pedagogice potocznej, na doświadczeniu społecznym co do (d) roli rówieśników w budowaniu tożsamości, umiejętności współpracy, a przede wszystkim wizji świata i działania w nim (T. Szlendak, 2009, 2013; ale też zob. obecne protesty młodych kobiet – choć nie tylko – a także głosy uczniów licealistów dot. niektórych wypowiedzi obecnego Ministra Edukacji i Nauki).
Relacje nauczycielsko-uczniowskie są jakby poza zasięgiem szybkiego wprowadzenia do klas szkolnych. Z jednej strony wystarczy zmienić je przez samych nauczycieli. Niekoniecznie. Przede wszystkim, pamiętać musimy o tym, że relacje te są głęboko zakorzenione w nauczycielskich osobowościach, ich osobistych doświadczeniach i preferencjach. To samo zastrzeżenie dotyczy uczniów, a nawet ich rodziców, ale też władz szkolnych!
Względne łatwo możemy jednak zmieniać natężenie działań eksperymentalnych i doświadczalnych na lekcjach. Zmierzać ku uczeniu budowania własnej wiedzy na podstawie własnych działań badawczych oraz obserwacji i analizie ich skutków. Mamy tutaj na uwadze głównie refleksje nad własnych działaniem i jego skutkami – działaniem zaplanowanym w eksperymentach (dotyczy to także planów w życiu codziennym…) oraz działaniem okazjonalnym w naszym życiu codziennym. Dodajmy jeszcze, że eksperyment to także działanie/operowanie słowem – eksperyment myślowy – inspirowany myślą i wewnętrznymi strukturami, gdyż w eksperymencie najważniejsze jest myślenie – zanim się pomyśli (DiYanni, 2016) – analiza sytuacji wyjściowej oraz projektowanie, potem dopiero następuje działanie, wytyczone myśleniem – w gruncie rzeczy – następuje tu przed samym działaniem eksperymentalnym – operowanie głównie słowem…no i też obrazami…
Proponujemy zatem do obejrzenia łącznie 75 filmów dotyczących przedmiotów ścisłych (do każdego przedmiotu 15 filmów, jednominutowych): biologii, chemii, fizyki, geografii oraz matematyki.
Zakładamy, że uczniowie mogliby – po obejrzeniu wybranego filmu – opisać go i przesłać opracowanie do grupy młodszej, prosząc o podawanie dalszych przykładów – czy nawet proponować przygotowanie ilustracji filmowej. Jedna grupa uczniów mogłaby także zorganizować dyskusję nad dalszymi przykładami – czy nawet projektami filmów czy instalacji, w celu ich lepszego wyjaśnienia.
- Dehaene S. (2009) Reading in the Brain. The new Science of how we read, Penguin Group, New York
- DiYanni R. (2016) Pomyśl, zanim pomyślisz. Myślenie krytyczne i kreatywne, PWN, Warszawa
- Hammond C. Does reading fiction make us better people? BBC Future, 3 June 2019
- Dylak S., Kształtowanie (się) kompetencji językowych uczniów w integracji z edukacją przyrodniczą, w: Konteksty Pedagogiczne, nr 1(8) 2017
- Everett D., (2018), Język. Narzędzie kultury, Wyd. Copernicus Center, Kraków
- Everett D., (2019) Jak powstał język. Historia największego wynalazku ludzkości, Prószyński i S-ka, Kraków
- Hattie J., 2012, Visible learning for teachers, Routledge, Abington
- Lundborg G., (2014) The hand and the brain, Springer-Verlag, London
- Palfrey J., Gasser U., Born Digital. Understanding the first generation of digital natives, Basic books, New York
- Rutherford A. (2019) Księga Ludzi. Opowieść o tym jak staliśmy się nami, Prószyński i S-ka, Warszawa
- Szlendak T. (2013), Kultura nadmiaru w czasach niedomiaru. „Kultura Współczesna” nr 1.
- Szlendak T. (2009) Kto wychowuje twoje dziecko? Focus, 20/04/09
- Tomasello M. (2015) Historia naturalna ludzkiego myślenia, Copernicus Center, Kraków
- Tomasello M., (2016) Dlaczego współpracujemy, Wyd. Copernicus Center, Kraków
Bibliografia
- Ciesielska B., Kowalczyk, A. (2016). Tam, gdzie matematyka, sztuka i magia łączą swoje siły, czyli słów kilka o origami. [online] : http ://www.deltami.edu.pl/temat/matematyka/geometria/2016/06/21/Tam gdzie_matematyka_sztuka/ [dostęp z dn. 1 kwietnia 2021].
- Delta Edu [portal]. [online] http://www.deltami.edu.pl/delta/archiwum/ [dostęp z dn. 1 kwietnia 2021].
- Dzień Delty [portal]. [online] https://emi.wmi.amu.edu.pl/dzien-delty/ [dostęp z dn. 1 kwietnia 2021].
- Freudenthal H. (1966). Rola intuicji geometrycznej we współczesnej matematyce. [w:] Roczniki Polskiego Towarzystwa Matematycznego Seria II: WIADOMOSCI MATEMATYCZNE IX, s. 83-87.
- Gołąb T. (1993). Origami w pracy dydaktyczno-wychowawczej. Życie Szkoły,nr 8.
- Mason J., Burton L., Stacey K. (2005). Matematyczne myślenie, Warszawa, WSiP.
- Jaszuńska J. (2017). Niemożliwe wycinanki. Delta. [online]s http://www.deltami.edu.pl/temat/matematyka/geometria/2017/03/27/Niemozliwe_wycinanki/ [dostęp z dn. 1 kwietnia 2021].
- Juskowiak E. (2019). “Using geometry, justify (…)”. Readiness of 14-year-old students to show formal operational thinking. Proceedings of the Eleventh Congress of the European Society for Research in Mathematics Education, ed.: Jankvist, U. T., Van den Heuvel-Panhuizen, M., & Veldhuis, M. , Freudenthal Group & Freudenthal Institute, Utrecht University and ERME.
- Kędzierska M. (2018). Kształtowanie intuicji geometrycznej u uczniów szkoły podstawowej. Praca magisterska. Promotor – dr Edyta Juskowiak. UAM Poznań.
- Ma S., Spector J.M. (2019). Inquiry and critical thinking skills for the next generation: from artificial intelligence back to human intelligence. Smart Learning Environments volume 6, Article number: 8.
- Niss, M. (2003). Quantitative Literacy and Mathematical Competencies, Quantitative Literacy. Why Numeracy Matters for Schools and Colleges. Proceedings of the National Forum on Quantitative Literacy held at the National Academy of Sciences in Washing-ton, D.C. on December 1–2, 2001, Madison B.L., Steen L.A. (ed.), s. 215–220
- Piaget J. (1966). Origins of Intelligence in Children, Warszawa, PWN.
- Piaget J. (1966). Child Psychology, Warszawa, PWN.
- Piaget J. (1977). Where Education is Going, Warszawa, Wydawnictwo Naukowe PWN.
- Polcyn A. (2019). Rola origami w nauczaniu geometrii. Praca dyplomowa. Promotor – dr Edyta Juskowiak. UAM Poznań.
- Polya G. (2009). Jak to rozwiązać?, Warszawa, Wydawnictwo naukowe PWN.
- Rosiak D.W. (2019). Programy IT wspierające kształtowanie wyobraźni przestrzennej u uczniów na poziomie szkoły podstawowej. Praca dyplomowa. Promotor – dr Edyta Juskowiak. UAM Poznań.
- Suszek A. (2018). Origami w procesie kształtowania pojęć geometrycznych na lekcjach matematyki. Praca dyplomowa. Promotor – dr Edyta Juskowiak. UAM Poznań.
- Turanu S. (1990). Wykłady o nauczaniu matematyki, Warszawa, PWN.
